Exponential functions are fundamental in mathematics, representing growth or decay rates․ Worksheets with answers in PDF format provide structured practice for graphing and analyzing these functions, enhancing understanding of their behavior and real-world applications․
Definition and Basic Properties
An exponential function is of the form ( y = ab^x ), where ( a ) and ( b ) are constants, and ( b > 0 ), ( b
eq 1 )․ These functions are characterized by their rapid growth or decay․ The base ( b ) determines the direction: if ( b > 1 ), the function grows; if ( 0 < b < 1 ), it decays․ The y-intercept is ( a ), and the x-intercept is absent since exponential functions never touch the x-axis․ They have a horizontal asymptote at ( y = 0 ) and a domain of all real numbers, making them essential for modeling real-world phenomena like population growth and radioactive decay․
Importance of Graphing Exponential Functions
Graphing exponential functions is crucial for visualizing their behavior, identifying key features like asymptotes and intercepts, and understanding their real-world applications․ By plotting these functions, students can observe how growth or decay occurs over time․ This skill is essential for solving problems in fields such as biology, physics, and finance․ Worksheets with answers provide a structured way to practice graphing, ensuring mastery of this fundamental concept․ They also help in developing analytical skills, enabling students to interpret and predict trends effectively․ Regular practice enhances problem-solving abilities and conceptual clarity․

Characteristics of Exponential Function Graphs
Exponential function graphs exhibit distinct features, including horizontal asymptotes, consistent increasing or decreasing behavior, and smooth, curved shapes․ These characteristics help identify growth or decay patterns․
Increasing and Decreasing Functions
Exponential functions can either increase or decrease based on their base․ If the base b > 1, the function is increasing, meaning as x increases, the output grows rapidly․ Conversely, if 0 < b < 1, the function decreases, showing decay over time․ Worksheets help identify these patterns by analyzing key points and asymptotes, ensuring students understand the behavior of exponential growth and decay models․ This knowledge is crucial for real-world applications in fields like finance and biology․
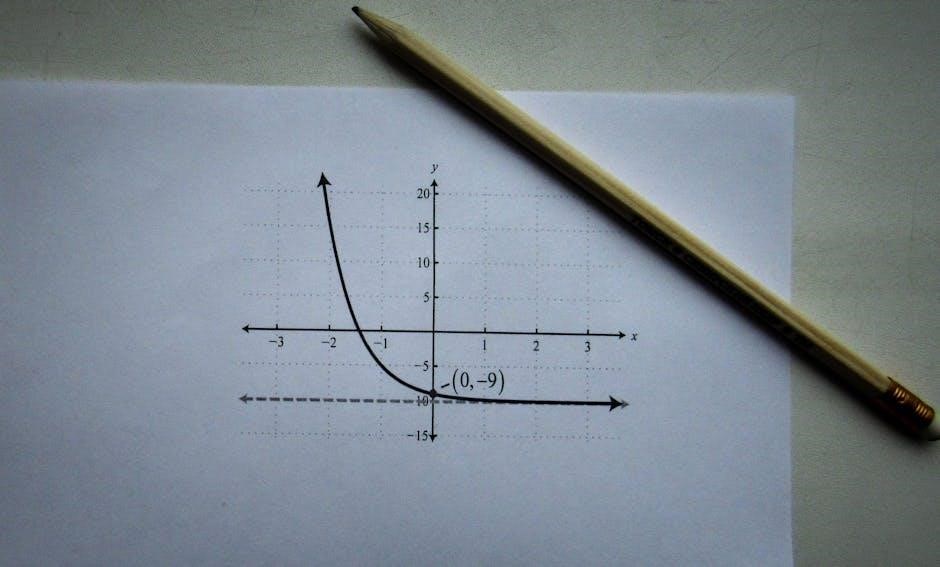
Exponential functions often have horizontal asymptotes, typically at y = 0 or y = a, depending on the function’s form․ These asymptotes indicate the behavior of the function as x approaches infinity or negative infinity․ Worksheets guide students in identifying these asymptotes and understanding end behavior, which is crucial for sketching accurate graphs․ For example, functions like y = ab^x approach their asymptotes as x becomes very large or very negative, shaping the overall appearance of the graph․ This concept is vital for analyzing growth and decay patterns in real-world scenarios․ The domain of exponential functions is all real numbers, meaning x can take any value․ The range, however, is typically y > 0 for functions of the form y = ab^x․ Worksheets help students identify these properties, ensuring they understand how exponential functions behave across their entire domain and range․ This knowledge is essential for graphing and interpreting real-world applications, such as population growth or radioactive decay, where understanding the function’s limits is critical․ Worksheets often include exercises to determine domain and range, reinforcing these foundational concepts․ Step-by-step graphing involves creating input-output tables, identifying asymptotes, determining domain and range, and plotting key points to ensure accuracy and understanding of exponential behavior․ Creating input-output tables is a practical method for graphing exponential functions․ By selecting specific x-values and calculating corresponding y-values, students can identify patterns and behavior․ For example, choosing x = -2, -1, 0, 1, 2 provides a clear view of growth or decay․ These tables help in plotting key points accurately and understanding how the function behaves as x increases or decreases․ They also aid in identifying asymptotes and transformations, making the graphing process systematic and efficient․ Regular practice with such tables enhances problem-solving skills and conceptual clarity․ Identifying asymptotes is crucial when graphing exponential functions․ A horizontal asymptote, typically y=0 or y=a, indicates the behavior of the function as x approaches infinity or negative infinity․ For exponential functions of the form y = ab^x, the horizontal asymptote depends on the base b․ If b > 1, the asymptote is y=0 as x approaches negative infinity․ Worksheets often include problems where students identify and label asymptotes, ensuring a clear understanding of the function’s end behavior․ This skill is vital for accurately sketching and interpreting exponential graphs․ Regular practice reinforces this concept effectively․ For exponential functions of the form y = ab^x, the domain is always all real numbers, written as (−∞, ∞)․ The range, however, depends on whether the function is growing or decaying․ If b > 1, the function grows without bound, so the range is (0, ∞)․ If 0 < b < 1, the function decays, and the range is also (0, ∞) since y approaches zero but never reaches it․ Worksheets often include exercises where students identify and state the domain and range for various exponential functions, reinforcing their understanding of these fundamental properties․ This practice helps in accurately graphing and interpreting exponential relationships․
Plotting key points is essential for accurately graphing exponential functions․ Start by identifying the y-intercept, which occurs at x = 0․ Use this point to anchor the graph․ Next, create a table of values to find additional points, ensuring a balance of positive and negative x-values․ For exponential growth, points rise steeply, while decay models approach zero․ Labeling these points helps in sketching the curve smoothly․ Worksheets often include exercises where students plot key points, identify asymptotes, and verify their graphs using technology, reinforcing their understanding of exponential behavior and its visual representation․ This step-by-step approach ensures precision and clarity in graphing․ Exponential functions can undergo transformations like horizontal shifts, vertical stretches, and shrinks, altering their graphs․ Factors ‘a’ and ‘b’ dictate vertical and horizontal scaling, crucial for accurate graphing and interpreting․ Horizontal shifts modify the position of an exponential function’s graph along the x-axis․ For a function y = ab^(x-h), where h determines the shift, positive values move the graph right, while negative values shift it left․ Worksheets often include exercises where students identify and graph such transformations․ Answer keys provide solutions to verify accuracy, ensuring understanding of how horizontal shifts affect the function’s appearance and behavior․ These exercises are essential for mastering graph transformations and their applications․ Vertical shifts alter the position of an exponential function’s graph along the y-axis․ For a function y = ab^(x) + k, where k is the shift, positive values move the graph up, while negative values shift it down․ This transformation does not affect the horizontal asymptote but changes the vertical positioning of key points․ Worksheets often include exercises where students graph functions with vertical shifts and identify their effects․ Answer keys provide solutions to verify understanding, highlighting how vertical shifts modify the function’s appearance without altering its exponential growth or decay behavior․ Vertical stretches and shrinks modify the coefficient ( a ) in an exponential function ( y = ab^x )․ If ( |a| > 1 ), the graph is stretched vertically, making it steeper; If ( 0 < |a| < 1 ), the graph is shrunk, appearing flatter․ These transformations do not affect the horizontal asymptote, which remains at ( y = 0 )․ Worksheets often include exercises where students graph functions with varying coefficients and identify the effects of these transformations․ Answer keys provide solutions to verify understanding of how vertical stretches and shrinks alter the function's appearance while maintaining its exponential nature․
Horizontal stretches and shrinks are applied by adjusting the base ( b ) in an exponential function ( y = ab^x )․ If ( 0 < b < 1 ), the graph is stretched horizontally, slowing growth or decay․ If ( b > 1 ), it is shrunk, accelerating these processes․ Worksheets often include problems where students graph functions with different bases and identify how these transformations affect the curve․ Answer keys help verify correct identification of horizontal stretches and shrinks, reinforcing understanding of their impact on exponential behavior․ These exercises are crucial for mastering function transformations․ Exponential functions include growth models (y = ab^x) and decay models (0 < b < 1)․ Special cases and examples provide practical insights into real-world applications․
Growth models, represented by the equation y = ab^x, describe exponential growth where a is the initial value and b > 1 is the growth rate․ These models are widely used to analyze population growth, financial investments, and biological processes․ Worksheets with answers provide exercises to graph these functions, identify asymptotes, and solve real-world problems․ For example, students practice sketching graphs, determining domains and ranges, and interpreting growth patterns․ These activities enhance understanding of exponential behavior and its applications in various fields․ Decay models, represented by y = ab^x with 0 < b < 1, describe exponential decay․ These functions are essential for modeling decreasing quantities, such as radioactive half-life or depreciation․ Worksheets offer exercises to graph decay functions, identify asymptotes, and solve real-world problems․ Students practice sketching graphs, determining domains and ranges, and interpreting decay rates․ These activities enhance understanding of exponential decay and its practical applications in science and finance․ They also improve analytical skills for solving equations and interpreting data․
Special cases of exponential functions, such as y = 2^x and y = (1/2)^x, are often highlighted in worksheets․ These examples illustrate key differences between growth and decay models․ Worksheets include exercises where students match equations to graphs, identify asymptotes, and interpret real-world scenarios․ For instance, problems involving population decline or radioactive decay demonstrate practical applications․ These examples help students recognize patterns and understand how exponential functions behave under various conditions, reinforcing their ability to solve complex problems and interpret graphical data effectively․ Exponential functions model real-world phenomena like population growth, radioactive decay, and compound interest․ Worksheets help students apply these concepts to practical scenarios, enhancing problem-solving skills and understanding of natural processes․ Population growth is a classic example of exponential functions in real-world applications․ Worksheets often include exercises where students model population growth using exponential equations like ( y = ab^x )․ These exercises help students understand how populations grow rapidly over time, following an exponential pattern․ By graphing these functions, students can visualize growth trends and predict future population sizes․ Such problems reinforce the concept of exponential growth and its practical implications in biology and ecology, making abstract mathematical ideas more tangible and relevant․ Radioactive decay exemplifies exponential functions through the concept of half-life, where a substance’s mass decreases over time․ Worksheets often include decay models using equations like ( y = ab^x ) with 0 < b < 1․ Students graph these functions to observe the decay process and calculate remaining mass after specific periods․ These exercises help in understanding the mathematical principles behind half-life and their applications in science․ By solving such problems, learners grasp the exponential nature of decay and its relevance in fields like nuclear physics and medicine, bridging math with scientific phenomena․ Compound interest is a classic example of exponential growth, modeled by functions like y = ab^x․ Worksheets often include exercises where students calculate future values of investments and graph the growth over time․ For instance, questions might ask to determine the final amount in an account or the number of years required for an investment to double․ Graphing these functions helps visualize the accelerating growth of compound interest, making it easier to understand financial planning and wealth accumulation․ These exercises are essential for developing practical math skills applicable to real-world scenarios like savings and investments․ Worksheets typically organize exercises by difficulty, starting with basic graphing and evaluation, followed by transformations and real-world applications․ They include examples, solutions, and space for practice, ensuring comprehensive learning and assessment of exponential function concepts․ Worksheets often include a variety of exercises, such as graphing functions, evaluating expressions, and identifying asymptotes․ Students practice transforming exponential functions, solving growth and decay problems, and matching equations to graphs․ Word problems involving population growth and radioactive decay are common․ Additionally, exercises focus on determining domains, ranges, and identifying increasing or decreasing trends․ Some worksheets also include creating tables of values and verifying graphs using technology․ These diverse exercises cater to different learning styles and reinforce both theoretical and practical understanding of exponential functions․ Worksheets typically include exercises like sketching graphs of functions such as y = 4^x or y = 2^{-x}․ Students are often asked to identify asymptotes, determine domains, and state ranges․ Problems may involve creating input-output tables to plot key points, transforming parent functions, or matching equations to their graphs․ For example, graphing y = 3^x and identifying its asymptote or sketching y = (1/2)^x to show decay․ These exercises help students visualize exponential behavior and understand growth or decay patterns in real-world contexts․ The answer key provides detailed solutions to graphing problems, including step-by-step explanations for sketching exponential functions, identifying asymptotes, and determining domains and ranges․ Solutions often include verification steps using technology to ensure accuracy․ For example, answers may explain how to transform parent functions like y = ab^x or decay models like y = a(1-r)^t․ Each solution is designed to clarify common misconceptions and reinforce understanding of exponential behavior․ This section is invaluable for self-assessment and mastering graphing techniques․ Effective techniques include analyzing function behavior, plotting key points, identifying asymptotes, and using algebraic methods to verify solutions․ These strategies ensure accurate and efficient graphing of exponential functions․ Creating input-output tables is a practical method for identifying patterns in exponential functions․ By evaluating the function at specific x-values, students can observe how y changes, revealing growth or decay trends․ This approach helps in plotting key points accurately, which are essential for sketching the graph․ Tables also aid in identifying asymptotes and intercepts, providing a clear understanding of the function’s behavior․ Additionally, analyzing the ratios between consecutive y-values helps determine the base of the exponential function, reinforcing the relationship between the function’s equation and its graph․ Identifying transformations from exponential function equations involves analyzing the function’s structure․ The standard form y = ab^x reveals base b, growth factor a, and direction․ Horizontal shifts are indicated by terms like y = a(b)^{x-h}, where h shifts the graph left or right․ Vertical shifts appear as y = a(b)^x + k, moving the graph up or down by k․ Vertical stretches or shrinks are evident when a is not 1․ These transformations alter the graph’s appearance but retain its exponential nature, aiding in accurate plotting and interpretation of growth or decay patterns․ Technology is a powerful tool for verifying the accuracy of exponential function graphs․ By inputting the equation into graphing software or calculators, students can generate precise visuals to compare with their hand-drawn graphs․ Tools like Kuta Software and Infinite Algebra 2 provide interactive platforms to plot functions and check transformations․ This method ensures accuracy and helps identify any errors in manual graphing․ Additionally, technology allows for dynamic adjustments, enabling real-time exploration of how changes in the equation affect the graph’s appearance and behavior․ Worksheets provide structured practice, reinforcing conceptual understanding and problem-solving skills․ They offer practical exercises for graphing, evaluating, and transforming exponential functions, preparing students for real-world applications and academic success․ Worksheets on graphing exponential functions help students grasp core concepts, such as identifying asymptotes, determining domain and range, and analyzing growth or decay patterns․ By solving exercises, learners build a strong foundation in understanding how exponential functions behave and transform․ Interactive examples and step-by-step solutions provide clarity, enabling students to visualize and interpret function graphs effectively․ This structured practice enhances problem-solving skills and prepares students for real-world applications and advanced mathematical studies․ Graphing exponential functions worksheets equip students with essential problem-solving techniques․ By analyzing function behavior, identifying transformations, and solving real-world problems, learners enhance their critical thinking․ Exercises involve sketching graphs, determining asymptotes, and interpreting growth or decay models․ Answer keys provide immediate feedback, reinforcing correct methods and highlighting areas for improvement․ Regular practice builds confidence and proficiency, enabling students to tackle complex scenarios with accuracy and efficiency․ Mastering exponential functions through structured worksheets prepares students for advanced math․ These exercises build a strong foundation in function analysis, essential for calculus and logarithmic studies․ By understanding growth models and transformations, learners develop skills necessary for complex problem-solving․ Answer keys ensure accuracy, while varied exercises challenge students to apply concepts in diverse contexts․ This preparation fosters a smooth transition to higher-level mathematics, enabling students to approach advanced topics with confidence and a solid understanding of fundamental principles․ Explore recommended websites like Kuta Software and jmap․org for comprehensive graphing exponential functions worksheets․ These platforms offer interactive tools and downloadable PDFs to enhance your practice and understanding․ For effective practice, visit Kuta Software and jmap․org․ These websites provide high-quality graphing exponential functions worksheets with detailed solutions․ Kuta Software offers a free trial for generating custom worksheets, while jmap․org includes specific resources like F․IF․C․7 for exponential graphing․ Both platforms cater to various skill levels, ensuring comprehensive understanding․ Additionally, they offer interactive tools for visualizing functions, making learning engaging and practical․ Utilize these resources to master graphing, asymptotes, and domain/range analysis with ease and accuracy․ They are ideal for both classroom and self-study environments․ Interactive tools like Desmos and GeoGebra are excellent for visualizing exponential functions․ These platforms allow users to input equations and observe real-time graph updates, aiding in understanding function behavior․ Features such as sliders enable exploration of transformations like horizontal and vertical shifts․ They are ideal for experimenting with growth and decay models, providing immediate feedback․ Additionally, these tools support asymptote identification and domain/range analysis, making them invaluable for both students and educators․ Their accessibility and interactivity enhance learning, fostering a deeper grasp of exponential functions and their properties․ For comprehensive learning, additional practice materials are available, offering varied exercises on graphing exponential functions․ These resources include PDF worksheets with answers, ideal for self-assessment․ Exercises cover graphing, transformations, and solving real-world problems like population growth and radioactive decay․ Websites and educational platforms provide supplementary materials, such as Kuta Software’s Infinite Algebra 2 worksheets․ These tools offer detailed solutions and structured practice, enhancing problem-solving skills․ They cater to different learning levels, ensuring a thorough understanding of exponential functions and their applications․ Regular practice with these materials reinforces conceptual knowledge effectively․Asymptotes and End Behavior
Domain and Range of Exponential Functions

Graphing Exponential Functions Step-by-Step
Creating Input-Output Tables
Identifying Asymptotes
Determining Domain and Range
Plotting Key Points

Transformations of Exponential Functions
Horizontal Shifts
Vertical Shifts
Vertical Stretches and Shrinks
Horizontal Stretches and Shrinks

Common Types of Exponential Functions
Growth Models (y = ab^x)
Decay Models (y = ab^x with 0 < b < 1)
Special Cases and Examples
Real-World Applications
Population Growth and Exponential Functions
Radioactive Decay and Half-Life
Financial Applications (Compound Interest)

Worksheet Structure
Types of Questions and Exercises
Examples of Graphing Problems
Answer Key and Solutions

Techniques for Solving Graphing Problems
Using Tables to Identify Patterns
Identifying Transformations from Equations
Verifying Graphs with Technology

Benefits of Using Worksheets
Reinforcing Conceptual Understanding
Developing Problem-Solving Skills
Preparation for Advanced Mathematics

Additional Resources
Recommended Websites and Tools
Interactive Graphing Tools
Further Practice Materials
